From recursion to grammars

Abstract:

The list-of-integers example

Let's take a very simple syntax function that parses a list of integers: 

code_cxx/prs.cc

 1   // Parses a list of integers into the 'lst' argument.
 2   bool Parser::parse_int_list(std::list<string>& lst) {
 3     // First look for the opening '['.
 4     m_lexer->parse_white_space();
 5     if(m_lexer->peekChar() != '[') {
 6       return false;   // Fail.  This is not an int-list.
 7     }
 8     m_lexer->getChar(); // Skip the peeked character.
 9 
10     // Parse the first integer element.
11     // If it's not present, we just have an empty list, which is fine.
12     string s= m_lexer->parse_int_literal();
13     if(s.length() > 0) {
14       lst.push_back(s);
15 
16       // The following loop looks for the other elements in the list,
17       // each one preceded by a comma.
18       while(true) {
19         m_lexer->parse_white_space();
20         if(m_lexer->peekChar() == ',') {
21           m_lexer->getChar(); // Skip the peeked character.
22         } else {
23           break; // No comma => end of list.
24         }
25 
26         m_lexer->parse_white_space();
27         s= m_lexer->parse_int_literal();
28         if(s.length() <= 0) {
29            // Syntax error: comma should be followed by element.
30            break; // Stop the loop.
31         }
32 
33         lst.push_back(s);
34       }
35     }
36 
37     if(m_lexer->peekChar() != ']') {
38       // Syntax error: missing ']'.
39     }
40     m_lexer->getChar(); // Skip the peeked character.
41 
42     return true;
43   }

This function stores the parsed integers in an existing list, and returns true if it succeeds.

After writing dozens of these functions by hand, you will notice that they all share a lot of common code. As with our lex functions before, we would like to exploit these commonalities.

Syntax expressions

Here is the most obvious expression into which we can abstract our list-of-integers example: 

 1 '[' (int (',' int)* )? ']'

This abstract expression is known as a syntax rule, a syntax expression, or a parsing expression. A collection of them is known as a parsing expression grammar or PEG.

In general, a grammar is just a collection of syntax rules. A PEG has some additional specific properties, such as explicit ordering, which we talk about below.

The expression above may vaguely remind you of a regular expression, but that's only superficial. PEGs are much more powerful than regular expressions, because they have to parse a wider variety of input languages. The expression above reads more or less as follows:

If you read '?' as 'if', and '*' as 'while', you can almost produce the original function from this abstract expression. You can even let a code generator do it for you! There's a wide array of open source tools that produce parsers from short grammars fully automatically; we will look at a few such tools later.

One thing you may have noticed, is that the original calls to parse_white_space are not represented in our abstract expression. Most parsing frameworks allow you to define the white space characters of your input language explicitly, and then parse them automatically between any pair of tokens, so that you never have to worry about them again. That's another advantage of our new level of abstraction.

PEGs: rules with ordered alternatives

Our abstract expressions are always tried in a specific order. Let me introduce the concept of alternatives to show you what I mean.

We can write our earlier list-parsing expression in a completely different way: 

 1 list -> '[' (contents | empty) ']'
 2 contents -> int ',' contents | int
 3 empty ->

The '?' and '*' have disappeared, and instead we now have three expressions. What is going on?

First of all, we have named the expressions. The first one is called "list", because it tells us how to parse a list structure. The second is called "contents" because it parses the contents of the list, between the square brackets.

In our original expression, the '*' indicated a kind of iteration, corresponding to the while loop in the generated code. In our new set of expressions, we now use recursion instead of iteration: the "contents" rule calls itself recursively, parsing successive integers in each call. So: The original '*' is now implicit, hidden in recursion.

The '?' was used to express optional input, corresponding to an if in the generated code. It is now replaced by '|'.

You have, no doubt, noticed that the "contents" expression consists of a number of alternatives, separated by a vertical bar '|' which should be read as "or". But keep in mind that the alternatives are tried in the specified order. This is very important in the world of parsing: The wrong order will lead to incorrect results.

When parsing the contents of a list, we first try an int followed by a comma and more contents; if that fails, we try a single int; finally we try empty contents. With a different order for these alternatives, parsing will fail. For example, if we try a single 'int' first, we will then never be able to parse the comma and the rest of the list contents.

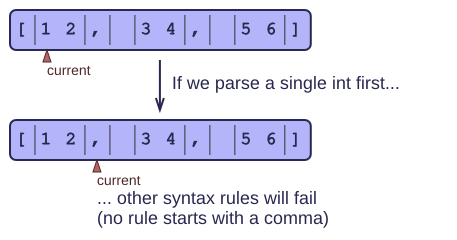
Empty contents are very easy to parse: they always succeed! For this reason, an 'empty' rule should always come last in the grammar.

Among all grammars, PEGs are the closest to our original hand-written syntax functions. They are also very natural for programmers, because our familiar programming languages also follow a strictly ordered execution path: they always try one thing before another, exactly in the order we tell them to.

Declarative grammars: rules with unordered alternatives

Many parsing frameworks take an additional step beyond PEGs: they allow the order of the alternatives to remain unspecified. The framework then somehow needs to figure out which alternative to try first, or it may even try all of them in parallel and take the best fit.

Instead of ordering the alternatives with an operator like '|', we now write out the alternatives explicitly: 

 1 list -> '[' contents ']'
 2 list -> '[' empty ']'
 3 contents -> int ',' contents
 4 contents -> int
 5 empty ->

You could still think of this as a PEG, if you decide that the rules must be tried in the order in which they appear in the grammar. But a non-PEG framework does not care about the order. The following is exactly the same grammar: 

 1 empty ->
 2 list -> '[' empty ']'
 3 list -> '[' contents ']'
 4 contents -> int
 5 contents -> int ',' contents

Tools such as Antlr or lex&yacc are smart enough to figure out what to do with such a grammar. You never have to worry about order again; the burden is now on the tools. The resulting grammars are said to be declarative because they only declare the rules, but do not impose a specific strategy for executing those rules.

Declarative grammars can sometimes be more readable than ordered ones. They even allow for left-recursive rules such as these: 

 1 contents -> contents ',' int
 2 contents -> int

We could never turn these rules into a "hand-written" syntax function directly, because the function would begin by calling itself! This would create an endless loop, a fun exercise for your patience. Certain parsing algorithms (bottom-up parsing in particular) manage to avoid the infinite loop. This can make grammars even more readable in some cases, because you no longer have to worry about left-recursion.

So it appears that declarative grammars have a lot of advantages over PEGs. Sadly, they also have a few downsides. The biggest one is that they introduce ambiguity.

Ambiguity

Consider the following grammar for integer lists: 

 1 contents -> contents ',' contents
 2 contents -> int

The first rule is subtly different from the earlier version: instead of allowing a single integer after the comma, it now allows an entire list. This doesn't seem like a big deal, but look at what happens when we parse the list [55, 66, 77]: 

 1 - list
 2   - '['
 3   - contents
 4     - contents
 5       - int 55
 6     - ','
 7     - contents
 8       - contents
 9         - int 66
10       - ','
11       - contents
12         - int 77
13   - ']'
14 
15 - list
16   - '['
17   - contents
18     - contents
19       - contents
20         - int 55
21       - ','
22       - contents
23         - int 66
24     - ','
25     - contents
26       - int 77
27   - ']'

These are two very different parse trees: the first one groups the 66 and 77 together, leaving the 55 dangling by itself. The second tree groups the 55 and 66 together. You could say that the first tree is "right-associative" and the second one is "left-associative". But here's the thing: both trees could be produced by our grammar, and both would be valid!

These issues become much, much more important when we start parsing arithmetic expressions such as '55+66*77'. If we don't succeed in associating the numbers with the correct operator, the parse tree will evaluate to the wrong value! It may compute (55+66)*77, which is incorrect. Solving the ambiguity in this case is crucial.

Ambiguity in lex expressions

Ambiguity is nothing new. We already encountered it in the article on lexing, although I did not make it explicit at that time. Take the following lex rule as an example: 

 1 int = [0-9]+

When parsing an input stream that contains the characters 1, 2 and 3 in succession, the lexer could find any of the following integers:

It cannot find an empty integer token, because the '+' in the rule means "at least one".

Lexers typically solve this ambiguity by being greedy: They scan as many input characters as they can find, never backtracking. This results in the longest possible token, which is '123' in our example. Note that this makes lexers very different from regular expression parsers, which do backtrack when they feel it's necessary.

Greediness is a kind of "external" strategy: it is part of the lexer itself, not part of the lex rules. The lex rules by themselves do not say anything about greediness or backtracking.

Ambiguity in syntax expressions

Syntax rules also have ambiguities, as we have seen. We could resolve these ambiguities by changing the behavior of the parser, or by changing the grammar itself. PEGs are an example of the first strategy. PEG parsers always try the rules in a predefined order, so you never have any ambiguities. In fact, many ambiguous grammars cannot even be expressed as PEGs because they are left-recursive. In any case, this anti-ambiguity strategy is external: it relies on the behavior of the parser, not on specific properties of the grammar itself.

Other techniques for removing ambiguity will be discussed in the next article. They will turn out to be decidedly not external: they require sophisticated changes to the grammar. This is often a difficult job to achieve, and it tends to turn beautiful, elegant grammars into an incomprehensible mess. For me, this is one of the main reasons to prefer PEGs over declarative parsing systems. Feel free to disagree.

Attaching actions to grammar rules

When given a grammar, the parser will try to match the input against each of the grammar's rules, one by one. It succeeds if all the input gets matched. But other than finding a match, or failing to do so, the parser does not actually produce anything yet. How do we make the parser more useful?

Most frameworks allow you to attach actions to each of the rules in a grammar. The actions are written in some programming language, and are executed whenever a rule is successfully matched against a piece of input. Here is a simple example that counts the number of elements in a list: 

 1 list -> '[' contents ']'              { count = 0 }
 2 list -> '[' empty ']'                 { count = 0 }
 3 contents -> int ',' contents          { ++count }
 4 contents -> int                       { ++count }
 5 empty ->

This is pretty much the same as our previous grammar, but this version has actions, shown between curly braces, which set up a counter and increment it whenever a list element is found.

Actions are very flexible. You can implement calculators, interpreters, syntax transformations, semantic analysis and many other tools directly in the grammar file, by attaching the appropriate actions to specific rules.

The biggest downside is that the grammar gets polluted with more and more of these actions, making it less readable and less maintainable. Left-factoring and other grammar transformations are difficult enough without having to worry about the associated actions.

Worse, if you need more than 1 tool for the same input language, you have to write two versions of the same grammar, each with its own set of actions. This is unworkable. In practice, you will obviously write only a single grammar, and you will implement actions that create a data structure such as a syntax tree. This tree is a nicely structured version of the input; you can then write several tools that traverse the tree or transform it. In other words, you use the grammar only to create a tree, and then you write "actions" as separate operations on that tree rather than directly on the grammar.

Most of the existing parsing frameworks do not help you in this area. You have to implement your own tree structure, and you have to write your own actions to create the tree nodes and fill them with data from the input. The OMeta framework offers some assistance in creating such nodes. A more practical approach is to use schema-based parsing. Read on.

Schemas

We have already come a long way, gradually abstracting from hand-written syntax functions to PEGs, then declarative grammars, and then grammars with actions to create a data structure. But we can also look at this in reverse: why don't we start from the data structure, and then write our syntax rules around it? This is the basic idea behind schema-based parsing. It's a different approach, and it leads to cleaner syntax trees. Let me explain.

Grammars have a tendency to introduce many new rules (often called "non-terminals") which serve no other purpose than to make the grammar right-recursive, or unambiguous, or otherwise more suitable for parsing. We have introduced the contents rule in the examples above, only because we needed a rule that could call itself recursively. The resulting grammar contains more rules than we want, and it creates a tree structure with more nested levels than we care for. We don't care about the distinction between a list and its contents, but we have to due to the limitations of grammars.

Instead, let's focus on the syntax tree that we want. We want to describe a set of classes from which tree nodes can be instantiated. We then write our syntax rules based only on those classes, without introducing unnecessary extra rules. Here's what it would look like in an imaginary object-oriented language: 

 1 // The parser will create List instances and fill them with elements.
 2 class List {
 3    // Each List node contains a list of children,
 4    // each of which represents a single integer from the input.
 5    child list<Element> elements;
 6 
 7    syntax: '[' elements*, ']'
 8 }
 9 
10 class Element {
11    int value;
12 
13    syntax: [0-9]+
14 }

This is only a sketch, but I hope it gets the basic idea across. The world has been flipped inside-out: Instead of a bunch of rules with node-creating actions attached to them, we now have a bunch of node classes with rules embedded in them. This collection of classes is called a schema. It focuses entirely on what the target tree will look like, rather than starting from what the input language looks like.

Look at the syntax rule embedded in the List class: 

 1 '[' elements*, ']'

This is a very PEG-like rule, but with a twist: It refers to elements, a data member of the class we're parsing! From the type of this data member (list<Element>), the parser knows that it should parse zero or more instances of the Element class, separated by commas. The "zero or more" is dictated by the '*', and the comma separator is dictated by, well, the comma (it's right there after the '*'). This is the shortest syntax rule for integer lists that we have seen so far, and it comes nicely packaged with the description of the resulting tree structure.

We no longer need to attach actions to grammar rules; The "default action" of the schema-based parser is to create a tree. We are then free to perform further operations on the tree, transforming it in any way we want. In many cases, this is much more natural because we no longer need artificial rules to keep the grammar-based parser happy.

For a more in-depth example, read the article on schemas and syntax trees.

Conclusion:
Previous: How to parse by hand
Next: Up and down the parsing spectrum