-
On top of the
InputStreamabstraction, we have now written a lexer which groups characters into short strings called tokens. - The lexer implements a set of lex functions which return tokens if they succeed. If they fail, they do not skip any input. This makes it easier to string the lex functions together (no pun intended).
- For some languages, we can pre-tokenize the input. In that case, the lexer becomes a separate step before the rest of the parser.
- A code generator can turn abstract lex expressions into lex functions automatically, saving a lot of development effort.
Scan if you can
- We have written an abstraction layer to access the characters in the input stream.
- We now group these characters into small strings called tokens, to provide more abstraction to the higher layers of our parser. This process is known as lexical analysis.
- Some programming languages make it hard or even impossible to do lexical analysis up front. We will look at some examples, including the most horribly un-lexable language of all: Fortran.
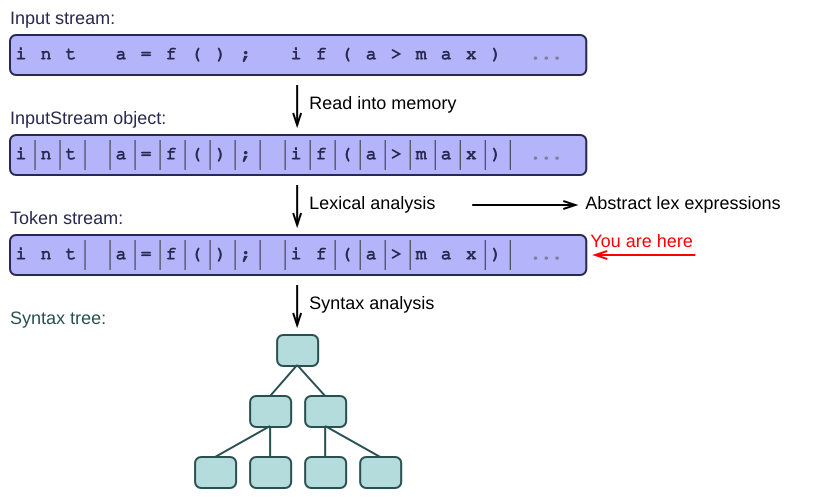
From one stream to another
Lexical analysis takes a stream of characters and produces a stream of tokens. This new stream then serves as input to the next stage of the parsing process.
Tokens are short strings containing 1 or more characters that we can treat together as a unit. Each of them also stores what kind of token it is: an identifier, an integer literal, an operator, ...
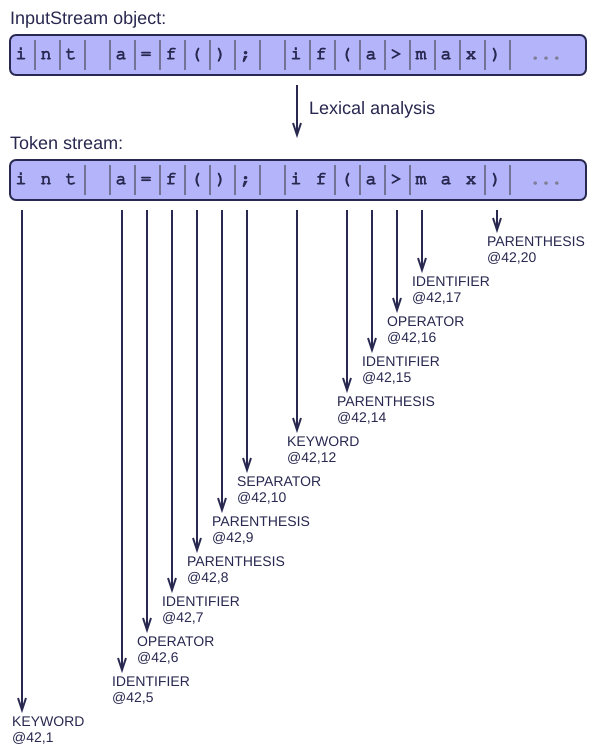
Some simple rules to follow
On top of the InputStream class of the previous article, we now write some lex functions that produce individual tokens.
The main rule for such a lex function is:
-
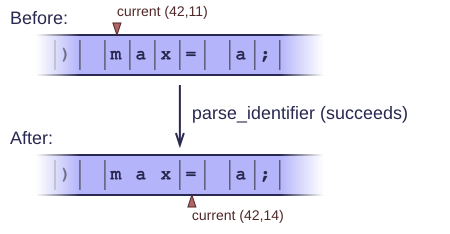
Either it succeeds and returns the token it found. It skips the corresponding input characters, so that the next function we call can immediately read the next characters after the token.
-
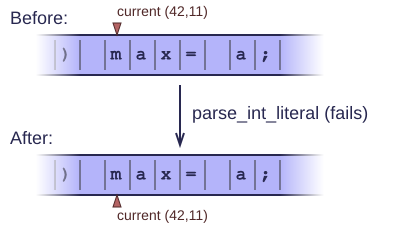
Or it fails and returns an empty or invalid token. It leaves the input exactly as it was, so that we can try another kind of token without explicitly having to backtrack first.
By following these rules, we make life easier for ourselves, as we will see in the coming examples.
Some examples in C++
Building on our previous code, we first write a class called Lexer, which holds our good old InputStream as a member. For convenience, we give this new class the same set of functions as InputStream itself (they just dispatch to the underlying member):
code_cxx/prs.cc
1 // Turns a stream of characters into a stream of tokens. 2 // The tokens are simply created on demand and returned as strings; 3 // they are not explicitly stored in a list of tokens. 4 class Lexer { 5 private: 6 InputStream* m_input; // Assume only 1 input stream, not a stack of them. 7 public: 8 Lexer(const char* filename) { 9 m_input= new InputFile(filename); 10 } 11 12 ~Lexer() { 13 delete m_input; 14 } 15 16 // Helper functions. 17 int getLineNumber() { return m_input->getCoord().m_lineNumber; } 18 int getColumnNumber() { return m_input->getCoord().m_columnNumber; } 19 20 // Access to the underlying input stream: just dispatch to 'm_input'. 21 // When using a stack of input streams: dispatch to top of stack. 22 const Coord& getCoord() { return m_input->getCoord(); } 23 void setCoord(const Coord& c) { m_input->setCoord(c); } 24 char getChar() { return m_input->getChar(); } 25 char peekChar() { return m_input->peekChar(); } 26 bool isEol() { return m_input->isEol(); } 27 bool isEof() { return m_input->isEof(); } 28 29 // ... 30 };
Instead of a single InputStream member, the class could also have a stack of them, as explained in the previous article. Here we stick to a single stream, to make the examples easier to follow.
Here is a simple function that finds spaces and newlines in the input and skips them:
code_cxx/prs.cc
1 int Lexer::parse_white_space() { 2 int start_col= getColumnNumber(); 3 while(peekChar() == ' ' || peekChar() == '\n' || peekChar() == '\r') { 4 getChar(); // Note that 'getChar' skips the character, but 'peekChar' does not. 5 } 6 return getColumnNumber() - start_col; // Return number of characters skipped. 7 }
This function returns the number of spaces it skipped. When 0, the input is still at exactly the same coordinate as before the function was called. So this little function obeys the rules we agreed on above.
Lex functions can return true when they succeed and false when they fail, or they can return the number of characters they munched (as in the example). More commonly though, a lex function returns the actual token it found. Here's an example that reads and returns an integer literal:
code_cxx/prs.cc
1 string Lexer::parse_int_literal() { 2 string result; 3 while(true) { 4 if(!isDigit(peekChar())) break; 5 result += getChar(); 6 } 7 return result; 8 }
This function returns a small string containing the digits of the integer literal it finds in the input stream. If it fails to find any digits, it returns an empty string and does not skip any characters, as agreed.
Now here is a function that tries to find a floating point literal in the input:
code_cxx/prs.cc
1 string Lexer::parse_real_literal() { 2 Coord start= getCoord(); // Store the starting coordinate. 3 4 string result= parse_int_literal(); // Use our earlier function. 5 if(result.size() == 0) 6 return string(""); // No digits found. 7 8 if(getChar() != '.') { 9 setCoord(start); // Backtrack to the beginning. 10 return string(""); 11 } 12 result += '.'; 13 14 string part2= parse_int_literal(); // Our earlier function again. 15 if(part2.size() == 0) { 16 setCoord(start); // Backtrack to the beginning. 17 return string(""); 18 } 19 result.append(part2); 20 21 return result; 22 }
This is our first example of backtracking. We start by storing the current coordinate. If we fail to find any of the 3 parts of the literal (an int, a dot, and another int), we backtrack to the stored coordinate so that we satisfy the agreement: when we fail, we don't skip any input. OK, you're right: we do skip some characters at first, but then we forget them again by moving back to our original coordinate. So the net effect is that we don't skip anything.
Also note that we can look for the '.' right after calling parse_int_literal the first time, without having to adjust our coordinates explicitly. Why? Because parse_int_literal already adjusted the coordinates and skipped the digit characters, following its contract as a lex function. You see, if every lex function sticks to the rules, writing a lexer is a breeze.
Some examples in C#
Building on our earlier C# code, here is an example of a familiar lex function:
1 public string parse_int() { 2 Line lin = GetLine(); // Get the current input line. 3 if (lin == null) { 4 // At end of file, we fail to parse an int literal. 5 // We fail by returning an empty string (and not skipping any input characters). 6 return ""; 7 } 8 9 if (!IsDigit(lin.txt[coord.col])) { 10 return ""; // Fail: return nothing, skip nothing. 11 } 12 13 int start_col = coord.col; 14 ++coord.col; 15 while ((coord.col < lin.txt.Length) && IsDigit(lin.txt[coord.col])) { 16 ++coord.col; // Skip the digits. 17 } 18 19 return lin.txt.Substring(start_col, coord.col - start_col); // Return the literal we found. 20 }
As you can see, the main idea is always the same even if the details differ. We skip the characters when we succeed, or skip none when we fail.
But this time, we have to do our own coordinate shuffling, since we decided not to do it in the InputStream before. The increments on 'coord.col' are explicit here, and we also explicitly access the contents of the line (lin.txt[coord.col]). The C++ example did not need this, because the InputStream already took care of the coordinates in its lower-level getChar method. You can clearly see that the C# version is more verbose (and more error-prone!), so this is a good argument for hiding as much of the low-level details as possible in the InputStream class. Still, the higher layers won't know the difference, so the work is still contained inside our lexer, which is acceptable.
One final example parses an identifier (a sequence of alphanumeric characters that can be used to identify a variable or other entity in a program):
1 public string parse_identifier() { 2 Line lin = GetLine(); 3 if (lin == null) { 4 return ""; 5 } 6 7 if (!IsLetter(lin.txt[coord.col])) { 8 return ""; // An identifier has to start with a letter, not a digit. 9 } 10 11 int start_col = coord.col; 12 ++coord.col; 13 while ((coord.col < lin.txt.Length) && IsLetterOrDigit(lin.txt[coord.col])) { 14 ++coord.col; 15 } 16 17 return lin.txt.Substring(start_col, coord.col - start_col); 18 }
Compare this to the 'parse_int' example above. You will see a lot of similarity. In fact, apart from a few differences in names, the functions are practically identical! Being good programmers, we see an opportunity here to save ourselves a lot of work. Instead of writing all these functions by hand, we should generate them automatically from a much smaller representation. We will do that in a later section below.
The correct order makes a big difference
We need to be careful about the order in which we call our lex functions. Suppose we have the characters '12.34' in the input.
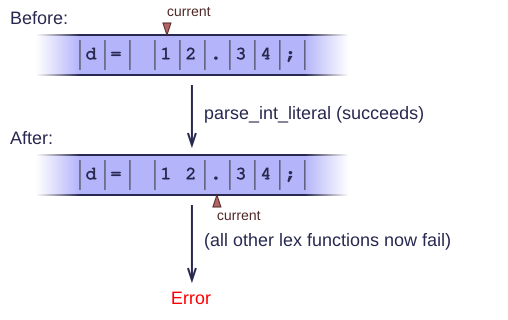
If we try an int-literal first, it will consume the '12' but leave the '.' alone. If we try a another lex function after that, it will fail to find anything meaningful (e.g. because no token begins with a dot). The only correct way to handle this, is to try a real-literal before an int-literal. Since every real-literal begins with an int-literal, we say that int is a prefix for real. Whenever we have such prefix ambiguities, the order in which we invoke lex functions determines how we resolve the ambiguity.
How to store the tokens
In the examples above, we read some characters from the input and return them in a string. We could also return a token object, an instance of a class containing the string plus additional information about the token (such as the token's coordinates, and its kind). For example, you could define an enumeration with all possible token kinds (IntLiteral, RealLiteral, StringLiteral, Identifier, Operator, ...). You could even use special token kinds to indicate end-of-file, end-of-line or other input conditions. The python parser even uses special tokens for indentation, to make sure that all the input lines are properly indented.
When we return tokens as objects, it becomes useful to store them in a list, containing all the tokens produced by the lex functions, in the correct sequence. The parser (the next stage in our parsing process) treats this list as a new stream containing tokens instead of individual characters.
One important question is what happens when we backtrack in this token stream. Do we have to forget the tokens and re-create them from raw characters, or can we re-use the tokens we already created before?
The answer is: it depends on the language we're parsing. Many languages have stable tokens. The tokens never change; they are completely independent of their context. These languages allow you to fully tokenize the input in advance. You can write a lexer that turns the character stream into a token stream in a completely separate step. The parser implements the next step and uses the token stream as its input. When backtracking, the parser backtracks in the token stream, re-using the tokens we already created.
Other languages have unstable tokens. The tokens depend on the context, and need to be re-examined after backtracking. Such languages are too ambiguous to allow full pre-tokenization; parsing and lexing need to happen in lock-step, not as fully separate phases. When backtracking, we may have to forget our tokens and recreate them from scratch.
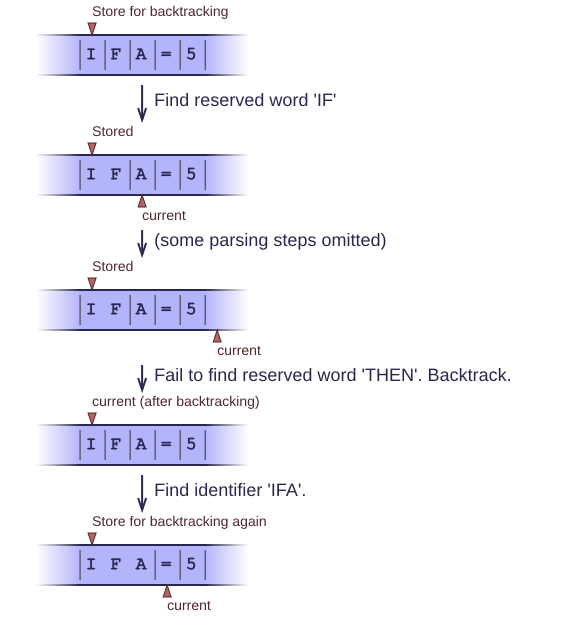
Fortran is a language with extremely unstable tokens. In Fortran, white space is irrelevant. No, really! The following two statements are exactly the same:
1 IF A = 5 THEN ... END IF 2 IFA=5THEN ... ENDIF
Of course this is horrible, but you'll have to deal with it if you need to parse Fortran programs. In particular, you have to be able to distinguish between the following two different statements:
1 IFA=5THEN ... 2 IFA=5
The first is an IF-statement, with condition 'A=5'. The second is an assignment to a variable named IFA. You don't know whether it's an assignment or an IF-statement until you see the THEN keyword. Upon backtracking, you'll need to re-tokenize the I, F and A characters because they belong to different tokens in both cases. So the only way to deal with this, is to re-create the tokens from scratch every time. Many parser frameworks cannot handle this kind of languages gracefully, because they assume that pre-tokenization is always possible. In real life, it isn't.
Extra features
I also want to mention that you can provide some useful features to the clients of the token stream. For example:
- You can make a lexer that completely hides the white space (spaces, tabs, newlines, ...). You just never store any white space tokens in the output stream. The higher-layer parser never even sees any white space.
- You can normalize the input. E.g. in case-insensitive languages, you can uppercase all the tokens, so that the parser does not have to worry about case sensitivity anymore.
- You can replace end-of-file, end-of-line and other special characters by tokens, so that the parser does not have to detect such special cases explicitly.
- You can glue consecutive tokens together into larger tokens. In C++, consecutive string literals are seen as a single longer literal. Languages like Cobol have continued lines which may break certain tokens into two pieces. By sticking them together, you free the higher-level parser from worrying about such details.
Abstract lex expressions
Above, we wrote a number of lex functions by hand. They contained a lot of boring, repetitive code; being good programmers, we would like to avoid this repetition somehow. Luck is on our side: it turns out that we can generate the functions automatically from much shorter lex expressions. The expressions contain exactly the same information as the earlier code, but in a shorter form. For comparison, I show the resulting code right after each expression (with details omitted for clarity). We begin with an integer literal:
code_cxx/prs.cc
1 // Expression for integer tokens: 2 int_literal= [0-9]+ 3 // Resulting code (details omitted): 4 string parse_int_literal() { 5 START(); 6 if(!isDigit(peekChar())) FAIL(); 7 while(isDigit(peekChar())) KEEP(getChar()); 8 SUCCESS(); 9 }
This code uses a few macros that I don't show explicitly. I could also have written them out completely (which makes more sense, since the code is generated anyway). But the use of macros better brings out the relationship between the generated code and the expression.
The START macro stores the current coordinate for later backtracking. The FAIL macro restores the coordinate and returns an empty string. In this particular example, backtracking is not really needed because we did not skip any characters yet. But our code generator may not be clever enough to figure that out, so it just always backtracks when failing. The KEEP macro adds a character to the current string, and the SUCCESS macro returns the whole string.
The expression for identifiers is only slightly more complex:
code_cxx/prs.cc
1 // Expression for identifiers: 2 identifier= [a-zA-Z][a-zA-Z0-9]+ 3 // Resulting code (details omitted): 4 string parse_identifier() { 5 START(); 6 if(!isLetter(peekChar())) FAIL(); 7 while(isLetterOrDigit(peekChar())) KEEP(getChar()); 8 SUCCESS(); 9 }
You can clearly see the similarities with the 'int' expression. The main difference is that the first character gets special treatment. The similarities between the two generated functions are also obvious.
Finally, we look at the rule for real literals. Note that it recursively invokes the rule for int literals:
code_cxx/prs.cc
1 // Expression for real literals: 2 real_literal= int_literal '.' int_literal 3 // Resulting code (details omitted): 4 string parse_real_literal() { 5 START(); 6 { 7 string result1= parse_int_literal(); 8 if(result1.size() == 0) FAIL(); 9 result.append(result1); 10 } 11 12 if(peekChar() != '.') FAIL(); 13 KEEP(getChar()); 14 15 { 16 string result3= parse_int_literal(); 17 if(result3.size() == 0) FAIL(); 18 result.append(result3); 19 } 20 21 SUCCESS(); 22 }
I hope you'll appreciate the extreme compactness of the lex expressions. Producing all that code by hand is much more work, and more error-prone. The abstraction from functions to expressions really pays off.
The expressions may remind you of regular expressions, but be careful: there are some important differences! When a regular expression engine fails to match its input against the expression, it backtracks and tries again within the same expression. For example, it could try to find a shorter match, sacrificing some characters to make the rest of the match more perfect. By contrast, most parsing frameworks use greedy matching, which always consumes as many characters as it can without ever backtracking to try other combinations. Greedy parsing is less advanced than regular expression matching, but more predictable, especially when running into ambiguities. Lex expressions are typically ambiguous, so we need greedy algorithms to make the parser deterministic.
Note that the 'real_literal' expression contains the 'int_literal' expression. We assume that our code generator prepends 'parse_' before each expression name before calling the corresponding function. So whenever you see 'int_literal' in an expression, the corresponding code says parse_int_literal().
To turn the simple lex expressions into actual functions, we need to write a code generator. This is an investment that pays off when you write a lot of parsers. Of course the code generator requires a parser to read the expressions in the first place! We already know how to write a parser by hand (or how to avoid writing one altogether), so we can use any of our earlier techniques to bootstrap the system. Writing a parser for our lex expressions should be a breeze. After that, the code generator makes it easier to write more advanced parsers.
Instead of writing your own lexer generator, you can of course use an existing one. Many generators are widely available and well-known. We may look at them in future articles.
